Dzisiejszy odcinek cyklu o funkcjach wypukłych pokaże, jak bardzo wiążą się one z wypukłymi podzbiorami płaszczyzny. Co to jest zbiór wypukły? Wypukłe są koła, prostokąty, wielokąty będące częściami wspólnymi skończenie wielu półpłaszczyzn itp. Istnieją oczywiście zbiory wypukłe nie mające takiej postaci.
Zacznijmy więc od sformalizowania pojęcia zbioru wypukłego. Tutaj odnoszę się tylko do płaszczyzny, ale należy mieć świadomość, że teorię zbiorów wypukłych uprawia się w ogólnych przestrzeniach liniowych. Niech więc $A$ będzie podzbiorem płaszczyzny. Szkolna definicja mówi, że $A$ jest zbiorem wypukłym, jeśli dla każdych dwóch punktów $a,b\in A$ odcinek $\overline{ab}$ jest zawarty w $A$. Jest ona bardzo intuicyjna, a jej bezpośrednią konsekwencją jest pewien warunek natury analitycznej. Otóż przyglądając się dokładnie poprzedniemu odcinkowi cyklu można zauważyć, że odcinek o końcach $(u_1, v_1)$ oraz $(u_2, v_2)$ składa się ze wszystkich punktów postaci\[t(u_1, v_1)+(1-t)(u_2, v_2)=\bigl(tu_1+(1-t)u_2, tv_1+(1-t)v_2\bigr)\,,\]gdzie $t\in[0,1]$.
Dlatego podzbiór $A$ płaszczyzny nazwiemy wypukłym, jeśli dla każdych $(u_1, v_1), (u_2, v_2)\in A$ zachodzi warunek\[\bigl(tu_1+(1-t)u_2, tv_1+(1-t)v_2\bigr)\in A.\]
Wróćmy teraz do funkcji. Niech $f:\I\to\RR$ będzie funkcją określoną w przedziale $\I\subset\RR$. Nadwykresem funkcji $f$ nazywamy zbiór\[\mbox{epi}(f)=\bigl\{(x,y):x\in\I\wedge y\xge f(x)\bigr\}\,,\]czyli zbiór wszystkich punktów $(x,y)$ leżących nad wykresem (lub na wykresie) funkcji $f$. Oznaczenie epi pochodzi od słowa epigraph.
Nadwykres przykładowej funkcji wypukłej pokazuje poniższy rysunek.
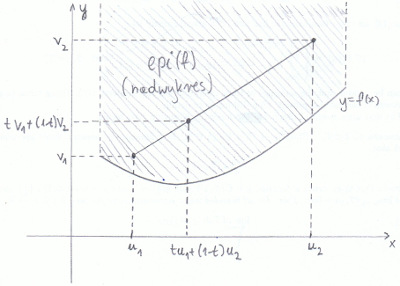
Widnieje na nim także odcinak łączący dwa wybrane punkty nadwykresu. Widzimy, że zawiera się on w tym nadwykresie. Nieprzypadkowo. Mamy bowiem następujące
Twierdzenie. Funkcja $f:\I\to\RR$ jest wypukła wtedy i tylko wtedy, gdy jej nadwykres jest zbiorem wypukłym.
Dla dowodu załóżmy najpierw, że nadwykres jest zbiorem wypukłym. Ustalmy $x_1,x_2\in\I$ oraz $t\in[0,1]$ i zauważmy, że punkty $\bigl(x_1,f(x_1)\bigr), \bigl(x_2,f(x_2)\bigr)$ należą do nadwykresu. Ponieważ jest on zbiorem wypukłym, to\[\bigl(tx_1+(1-t)x_2, tf(x_1)+(1-t)f(x_2)\bigr)\in\mbox{epi}(f)\,,\]skąd wnosimy, że\[tf(x_1)+(1-t)f(x_2)\xge f\bigl(tx_1+(1-t)x_2\bigr)\,,\]a ta nierówność definiuje funkcję wypukłą.
Załóżmy teraz, że $f$ jest funkcją wypukłą i ustalmy dowolne $(u_1, v_1), (u_2, v_2)\in\mbox{epi}(f)$ oraz $t\in[0,1]$. Oznacza to, że\[v_1\xge f(u_1)\quad\text{oraz}\quad v_2\xge f(u_2)\,.\]Mamy więc\[tv_1\xge tf(u_1)\quad\text{oraz}\quad (1-t)v_2\xge (1-t)f(u_2)\,.\]Po dodaniu tych nierówności stronami dochodzimy do nierówności\[tv_1+(1-t)v_2\xge tf(u_1)+(1-t)f(u_2)\,.\]Z wypukłości funkcji $f$ wynika, że\[tf(u_1)+(1-t)f(u_2)\xge f\bigl(tu_1+(1-t)u_2\bigr)\,,\]co w połączeniu z poprzednią nierównością daje nam\[tv_1+(1-t)v_2\xge f\bigl(tu_1+(1-t)u_2\bigr)\,,\]czyli\[\bigl(tu_1+(1-t)u_2, tv_1+(1-t)v_2\bigr)\in\mbox{epi}(f)\]dowodząc tym samym wypukłości nadwykresu.
Można też pokazać, że jeśli $A$ jest zbiorem wypukłym (na płaszczyźnie) takim, że dla każdego $x\in\I$ istnieje kres dolny zbioru $A_x=\bigl\{y\in\RR:(x,y)\in A\bigr\}$, to funkcja $f(x)=\inf A_x$ (kres dolny zbioru $A_x$) jest wypukła. Pozostawiam to jako ćwiczenie dla Czytelników.
Tak więc pojęcie funkcji wypukłej generuje nam rodzinę zbiorów wypukłych, a i zbiory wypukłe prowadzą nas do konstrukcji funkcji wypukłych. Te dwa pojęcia mocno się przenikają.
Oprócz funkcji wypukłych mamy też funkcje wklęsłe. Czy więc nadwykres funkcji wklęsłej jest zbiorem wklęsłym? Co to w ogóle jest zbiór wklęsły? Zapraszam do odpowiadania w komentarzach.
Mnie uczono, że zbiór wklęsły to taki, który nie jest wypukły. Idąc za tą sugestią, można z łatwością powtórzyć Pana rozumowanie dowodząc, że istotnie nadwykres funkcji wklęsłej jest zbiorem wklęsłym.
Analogiczne własności można zdefiniować dla „podwykresu” (definiując go analogicznie jako zbiór tych punktów płaszczyzny, które leżą pod wykresem danej funkcji). Tak więc „podwykres” funkcji wklęsłej jest wypukły i na odwrót – „podwykres” funkcji wypukłej jest zbiorem wklęsłym. Dowody są niemal identyczne. Można to szybko pokazać korzystając z tego co mamy już udowodnione. Bierzemy symetrię względem osi OX układu współrzędnych. Wówczas obrazem funkcji $f$ będzie oczywiście funkcja $-f$. Nietrudno zauważyć, że $f$ jest wypukła wtedy i tylko wtedy, gdy $-f$ jest wklęsła (i ogólniej $-f$ jest przeciwnej wypukłości co $f$). W takim razie biorąc pod uwagę fakt, że symetria jest izometrią oraz korzystając z tego co już wiemy o nadwykresie, mamy niemal za darmo dowody analogicznych własności dla „podwykresu”.
PS: Czy załączony rysunek jest odręczny? Jeśli tak, to gratuluję, bo jest bardzo staranny 😀
Rysunek wykonałem od linijki, krzywa od krzywika.
Jeśli zbiorem wklęsłym nazwiemy ten, który nie jest wypukły, to nie mogę się zgodzić z wklęsłością podwykresu funkcji wypukłej. Przecież funkcje liniowe są wypukłe. Wklęsłym będzie dopiero podwykres funkcji ściśle wypukłej.
Co ciekawsze, funkcja jest wklęsła wtedy i tylko wtedy, gdy jej podwykres jest zbiorem wypukłym. 🙂
Trochę się ubawiłem pytaniem o zbiór wklęsły…
A co to, co to to, co to tak…
Niestety bardzo często zapominamy, że dwa pojęcia, które semantycznie są przeciwne wcale nie wypełniają całego uniwersum. Tak jak między czarnym i białym jest całe mnóstwo nienazwanych barw, tak między funkcjami wypukłymi a wklęsłymi jest całe multum takich, których do żadnej z tych kategorii zaliczyć się nie da.
Szymon – prowokator próbuje wpuścić nas w maliny zbiorów wklęsłych, doskonale wiedząc, że takiego pojęcia raczej się nie używa (choć gdyby się uprzeć, można by tak nazwać podgraf funkcji wypukłej).
Z tym podgrafem to nie za bardzo ze względu na funkcje afiniczne.
A czy zbiór nie może być jednocześnie wklęsły i wypukły? Podobnie jak wypukłą i wklęsłą jest funkcja afiniczna?
Przy „definicji” zbioru wklęsłego podanej przez Mateusza zbiór epigraf sinusa byłby wklęsły (bo przecież nie jest wypukły, a to niestety obala całe „Twierdzenie” o odpowiedniości funkcji wypukłych i zbiorów wypukłych.
Okeślanie wklęsłym zbioru, który nie jest wypukły jest troche pozbawione sensu w kontekście funkcji wklęsłych. Jest mnóstwo funkcji, które nie są ani wypukłe ani wklęsłe, ale wtedy w myśl takiej „definicji” ich nadwykresy musiałyby byc zbiorami wklęsłymi, a zatem ona same musiałyby byc funkcjami wklęsłymi.
Strach sie bać. Nie próbujmy zatem używać na co dzień takiej definicji wklęsłości zbioru.
Ale w jedną stronę z założeniem ścisłej wypukłości da się to obronić.
Ja proponuję taką definicję: zbiór jest wklęsły jeśli jego dopełnienie jest zbiorem wypukłym. Dla funkcji wklęsłych (i ciągłych) mamy zachowaną analogię: nadwykres funkcji wklęsłej jest zbiorem wklęsłym. 🙂
To przenosi się też na znane ze szkolnej geometrii kąty wklęsłe.
Niestety, nie ma tak dobrze: funkcja $f:[-1,1]\to\mathbb{R}$ zadana wzorem $f(x)=-x^2$ jest wklęsła, ale jej nadwykres nie jest wklęsły w myśl tej definicji ;P